У математиці SO(3) — група обертань навколо фіксованої точки (початку координат) в тривимірному евклідовому просторі. Назва виникла через те, що ця група ізоморфна спеціальній ортогональній групі ступеня 3. За визначенням, обертання навколо початку координат — це перетворення, що зберігає початок координат, евклідову відстань (так що це ізометрія), і орієнтацію (тобто, об'єктивність простору). Будь-яке нетривіальне обертання визначається його віссю (лінія, що проходить через початок координат) і кутом. Поєднання двох обертань призводить до іншого обертання; кожне обертання має унікальне зворотне обертання; і тотожне відображення задовольняє визначенню обертання. Внаслідок зазначених вище властивостей усі обертання утворюють групу. Крім того, група обертань має таку природну структуру як многовид, для якого групові операції є гладкими; так що це насправді група Лі. Вона компактна і має розмірність 3.

Обертання це лінійні перетворення R³ і, отже, можуть бути представлені матрицями, щойно буде обраний базис R³. Зокрема, якщо ми виберемо ортонормований базис з R³, кожне обертання описується ортогональною матрицею 3х3 (тобто матриця 3х3 з дійсними елементами, які при множенні на транспоновану матрицю, призводять до одиничної матриці) з визначником 1. Група SO(3) визначається групою цих матриць при множенні матриць. Ці матриці відомі як «спеціальні ортогональні матриці», пояснюючи позначення SO(3).

Група SO(3) застосовується для опису можливої обертальної симетрії об'єкта, а також можливої орієнтації об'єкта в просторі. Його представлення відіграють важливу роль у фізиці, де вони призводять до виникнення елементарних частинок цілого спіну.

Крім того, що обертання зберігають відстані, обертання також зберігають кути між векторами. Це випливає з того, що стандартний скалярний добуток між двома векторами U і V (у евклідовому просторі) можна записати через їх довжину:

${\displaystyle u*v={\frac {1}{2}}{\Bigl (}\|u+v\|^{2}-\|u\|^{2}-\|v\|^{2}{\Bigr )}}$

Звідси випливає, що будь-яка довжина зберігає перетворення в R³, скалярний добуток, і, отже, кут між векторами. Обертання часто визначають як лінійні перетворення, що зберігають скалярний добуток на R³, що еквівалентно вимозі збереження відстані. Дивись класичну групу для обробки цього більш загального підходу, де SO(3) виступає як окремий випадок.

Кожне обертання відображає ортонормований базис з R³ на інший ортонормований. Як і будь-яке лінійне перетворення скінченновимірних векторних просторів, обертання завжди може бути представлене матрицею. Нехай R задане обертання. Що стосується стандартного базису e₁, e₂, e₃ з R³ стовпці R визначаються за формулами (Re₁,Re₂,Re₃). Оскільки стандартний базис ортонормований, а так як R зберігає кути і довжину, стовпці R утворюють інший ортонормований базис. Ця умова ортонормованості може бути виражена у вигляді

${\displaystyle R^{T}R=RR^{T}=I,}$

де RT означає транспонування, R і I є одиничною матрицею 3 × 3. Матриці, для яких виконана ця властивість, називаються ортогональними матрицями. Група всіх ортогональних матриць 3 × 3 позначається O(3), і складається з усіх власних і невласних обертань. Крім збереження довжини, власні обертання повинні також зберегти орієнтацію. Матриця буде зберігати або зворотню орієнтацію в залежності від того яким буде визначник матриці, позитивним або негативним. Для отримання ортогональної матриці R, зауважимо, що det R ^T= det R має на увазі (det R)² = 1, так що det R = ± 1. Підгрупа ортогональних матриць з визначником +1 називається спеціальною ортогональною групою, позначена як SO(3).

Таким чином, кожне обертання може однозначно представлятись ортогональною матрицею з одиничним визначником. Крім того, оскільки композиція обертань відповідає матричному множенню, група обертань ізоморфна спеціальній ортогональній групі SO(3). Невласні обертання відповідають ортогональним матрицям з визначником -1, і вони не утворюють групи, оскільки добуток двох невласних обертань складає правильне обертання.

Група обертань є групою під композицією функцій (що еквівалентно добутку лінійних перетворень). Це є підгрупою загальної лінійної групи, що складається з усіх оборотних лінійних перетворень реального координатного простору R³.

Група обертань неабелева (некомутативна). Тобто, результат двох обертань може відрізнятися залежно від порядку їх виконання. Наприклад, чверть оберту навколо осі X, за яким слідує чверть оберту навколо осі Y являє собою інший поворот, ніж обертання спочатку навколо Y, а потім — навколо X.

Ортогональна група, що складається з усіх власних і невласних обертань, породжується дзеркальними відображеннями. Кожне правильне обертання є композицією двох дзеркальних відображень, окремим випадком теореми Картана-Д'єдонне^{[прояснити]}.

Кожне нетривіальне власне обертання в 3-х вимірах фіксує унікальний 1-мірний лінійний підпростір R³, який називається віссю обертання (це теорема обертання Ейлера). Кожне таке обертання діє як звичайне 2-вимірне обертання в площині, що перпендикулярна цій осі. Оскільки кожне 2-вимірне обертання може бути задано кутом ф, довільне 3-вимірне обертання може бути задане за допомогою осі обертання разом із кутом обертання навколо цієї осі. (потрібно задати не тільки розташування, а й орієнтацію осі, та визначити напрямок обертання — за годинниковою стрілкою або проти годинникової стрілки відносно до заданої орієнтації).

Наприклад, обертання проти годинникової стрілки щодо позитивної осі на кут ф задається

${\displaystyle R_{z}(\phi )={\begin{bmatrix}\ cos\phi &\ -sin\phi &0\\\sin \phi &\cos \phi &0\\0&0&1\end{bmatrix}}}$.

З огляду на одиничний вектор n в R³ і кут φ, нехай R(φ,n) являє собою обертання проти годинникової стрілки навколо осі через n (з орієнтацією, визначеною n). тоді

• R (0, n) є тотожне перетворення для будь-якого n
• R (φ, n) = R(-φ, -n)
• R (π + φ, n) = R(π - φ, -n).

Використовуючи ці властивості, можна показати, що будь-яке обертання може бути представлене унікальним кутом ф в діапазоні 0 ≤ ф ≤ π і одиничним вектором n, таким, що

• n довільно, якщо φ = 0
• n єдино, якщо 0 <φ <π
• n єдина з точністю до знака, якщо ф = π (тобто обертання R(π, ± π) однакові).

Ця стаття є сирим перекладом з іншої мови. Можливо, вона створена за допомогою машинного перекладу або перекладачем, який недостатньо володіє обома мовами. Будь ласка, допоможіть поліпшити переклад. (жовтень 2019)

Група Лі SO (3) дифеоморфний дійсний проєктивний простір RP³. Розглянемо тверду кулю в R³ радіуса π (тобто, всі точки R³ на відстані π чи менше від початку координат). З урахуванням вищесказаного, для кожної точки в цій кулі відбувається обертання з віссю, що проходить через точку і початок координат, а також кут повороту, що дорівнює відстані від точки до початку координат. Ідентичне обертання відповідає точці в центрі кулі. Обертання на кути між 0 і -π відповідають точці на тій же осі, і відстані від початку координат проте на протилежному боці від початку координат. Проте питання полягає в тому, що два оберти через π і через -π однакові. Таким чином, ми ототожнюємо (або "склеюємо") діаметрально протилежні точки на поверхні кулі. Після цієї ідентифікації, ми приходимо від гомеоморфного топологічного простору до групи обертань.

Дійсно, куля з ототожненими діаметрально протилежними точками поверхні є гладким многовидом, і цей многовид дифеоморфний групі обертань. Він також дифеоморфний дійсному 3-мірному проєктивному простору RP³, так що останній може також служити як топологічна модель для групи обертань.

Ці ототожнення показують, що SO(3) зв'язний, але не просто зв'язаний. Що стосується останнього, в кулі з ототожненими діаметрально протилежними точками поверхні, розглянемо шлях, що йде від «північного полюса» через внутрішню порожнину до південного полюса. Це замкнутий цикл, бо північний полюс і південний полюс ототожнено. Цей цикл не може бути стягнутий в точку, бо незалежно від того, як деформовано контур, початкова та кінцева точки мають залишатися діаметрально протилежними, інакше цикл буде "розкриватись". З точки зору обертань, цей цикл являє собою безперервну послідовність обертань навколо Z-осі і закінчуючи обертанням ідентичності (тобто ряд оберту на кут ф, де φ пробігає від 0 до 2π).

Дивно, але якщо пройти цей шлях двічі, тобто, від північного полюса до південного полюса, а потім назад до північного полюса (враховуючи той факт, що північний і південний полюси ототожнені), а потім знову пройти від північного полюса на південний полюс, так що φ змінюється від 0 до 4 π, утворюється замкнутий контур, який може бути стягнутий у точку: спочатку перемістити шлях безперервно до поверхні кулі, все ще з'єднує північний полюс південний полюс двічі. Друга половина шляху може бути дзеркальною до діаметрально протилежної сторони без зміни траєкторії взагалі. Тепер у нас є звичайний замкнутий контур на поверхні кулі, що приєднує північний полюс до себе по великому колу. Це коло може бути зменшене до Північного полюса без проблем. Балійський трюк з пластиною і подібні трюки демонструють це на практиці.

Той же аргумент може бути виконаний в цілому, і це показує, що фундаментальна група SO(3) є циклічною групою порядку 2. У фізиці додатків, нетривіальність фундаментальної групи допускає існування об'єктів, відомих як спінор, і є важливим інструментом у розвитку теореми Паулі.

Універсальне накриття SO(3) є групою Лі називається Spin(3). Група Spin(3) ізоморфна спеціальній унітарній групі SU(2); також дифеоморфна до блоку 3-сфери S³ і може бути зрозуміла як група versors (кватерніонів з абсолютним значенням 1). Зв'язок між кватерніонами і обертаннями, зазвичай експлуатують в комп'ютерній графіці, пояснюється в кватерніонових і просторових обертаннях. Відображення S³ на SO(3), яке ідентифікує діаметрально протилежні точки S³ є сюр'єктивним гомоморфізмом груп Лі, з ядром {± 1}. Топологічно, ця карта є два до одного зв’язаного простору.

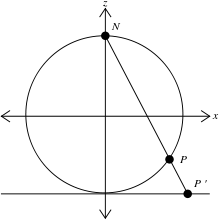
Точки P, за винятком північного полюса N , на сфері S = {( х , у , z ) ∈ ℝ³ : х² + у² + z² = 1/4} можуть бути введені один-до-одного бієкцію з точками S(P)=P на площині М і визначатись як z=-1/2,що можна побачити на фігурі. Відображення S називається стереографічною проєкцією. Нехай координати на М будуть (ξ,η) . Лінію L , що проходить через N і P можна записати

${\displaystyle L=N+t(N-P)=(0,0,1/2)+t((0,0,1/2)-(x,y,z)),t\in \mathbb {R} }$.

Присвоюємо z-координаті значення 1/2,знаходимо ${\displaystyle t={\frac {1}{z-{\tfrac {1}{2}}}}}$, отже

${\displaystyle S:S\rightarrow M\rightarrow P';(x,y,z)\mapsto (\xi ,\eta )=\left({\frac {x}{{\frac {1}{2}}-z}},{\frac {y}{{\frac {1}{2}}-z}}\right)\equiv \zeta =\xi +i\eta }$,

де, для подальшої зручності, площина М ототожнюється з комплексною площиною ℂ.

Пов'язана з кожною групою Лі, алгебра Лі це лінійний простір тієї ж розмірності, що і група Лі, закритий під білінійною змінною продукту званого дужкою Лі. Алгебра Лі SO (3) позначається so(3) і складається з усіх кососиметричних матриць 3 × 3. Це можна побачити шляхом диференціювання умови ортогональності, A^TA = I, A ∈ SO(3). Дужка Лі двох елементів so(3), як і для алгебри Лі кожної групи матриць, задається матричним комутатором [A₁, A₂] = A₁A₂ − A₂A₁, а це знову-таки кососиметрична матриця. Дужка Лі відображає суть продукту групи Лі в деякому сенсі більш точно за формулою Бейкера-Кемпбелла-Хаусдорфа.

Елементи so (3) є "нескінченно малими генераторами" обертань, тобто вони є елементами дотичного простору многовиду so(3) у одиничного елемента. Якщо R (φ, n) позначає обертання проти годинникової стрілки з кутом φ щодо осі зазначеного одиничного вектора n,

${\displaystyle {\operatorname {d} \over \operatorname {d} \phi }|R(\phi ,n)x=n\times {\mathsf {x}}}$,

для кожного вектора x в R³.

Група обертань цілком природно узагальнюється для n-мірного евклідового простору Rⁿ зі стандартною евклідовою структурою. Група всіх власних і невласних обертань в n вимірах називається ортогональною групою O ( n ), а підгрупа власних обертань називається спеціальною ортогональною групою SO(n), яка є групою Лі розмірності n( n - 1 ) / 2.

У спеціальній теорії відносності працюють у 4-вимірному векторному просторі, відомому як простір Мінковського. На відміну від евклідового простору, простір Мінковського має скалярний добуток невизначеного знаку. Можна визначити узагальнені обертання, що зберігають цей скалярний добуток. Узагальнені обертання відомі як перетворення Лоренца і група всіх таких перетворень називається групою Лоренца.

Група обертань SO(3) може бути описана як підгрупа E(^+) (3) , евклідова група з прямих ізометрій евклідової R³ . Ця більша група являє собою групу всіх рухів твердого тіла: кожен з них являє собою комбінацію обертання навколо довільної осі і зсуву вздовж осі, або інакше кажучи, це комбінація елемента з SO(3) і довільного зсуву.

Взагалі, групи обертання об'єкта є групою симетрії всередині групи прямих ізометрій; Іншими словами, перетин повної групи симетрії і групи прямих ізометрій. Для отримання хіральних об'єктів це теж саме, що повна група симетрії.

• Ортогональна матриця
• Матриця повороту
• Формула повороту Родрігеса
• Кватерніони і повороти простору
• Ейлерові кути