
Трику́тник в евклідовій геометрії — геометрична фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які їх сполучають. Трикутник з вершинами , , і позначається . Трикутник є многокутником і -симплексом. В евклідовій геометрії трикутник однозначно задає площину. Всі трикутники двовимірні.
Основні відомості про трикутники подано Евклідом у праці «Елементи» близько 300 до н. е.
Типи трикутників

Трикутники класифікують залежно від взаємних довжин їхніх сторін:
- Рівностороннім називають трикутник, в якого всі сторони мають однакову довжину. Всі кути рівностороннього трикутника також рівні і дорівнюють , а центри вписаного та описаного кіл збігаються. Рівносторонній трикутник ще називають правильним.
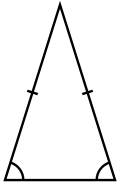
- Рівнобедреним називають трикутник, в якого дві сторони мають однакову довжину. Ці сторони називають бічними, третю сторону називають основою трикутника. У рівнобедреному трикутнику кути при його основі рівні.
- Різностороннім називають трикутник, в якого всі сторони мають різну довжину. Внутрішні кути різностороннього трикутника також різні за величиною.
Трикутники класифікують також залежно від їхніх внутрішніх кутів:
- Якщо один із внутрішніх кутів рівний (прямий кут), то трикутник називають прямокутним. Сторону, протилежну до прямого кута, називають гіпотенузою, а інші дві сторони — катетами.
- Якщо один із внутрішніх кутів більший ніж , то трикутник називають тупокутним.
- Якщо всі кути трикутника менші від , то трикутник називають гострокутним. Рівносторонній трикутник є гострокутним, але не всі гострокутні трикутники рівносторонні.
Точки і лінії, пов'язані з трикутником
Є сотні різноманітних побудов для визначення особливих точок всередині трикутника, які задовольняють деякі унікальні умови (див. у списку посилань перелік статей). Часто необхідно побудувати три прямі, пов'язані аналогічно з трьома сторонами (вершинами, кутами) трикутника, і тоді переконатись, що вони перетинаються в одній точці. Важливим інструментом для перевірки цього є теорема Чеви, яка дає критерії для визначення конкурентності прямих. Подібно до цього лінії, пов'язані з трикутником, часто будують після перевірки, що три аналогічним чином отримані точки є колінеарні — теорема Менелая дає для цього випадку загальний критерій. Тут подані тільки ті побудови, що найчастіше трапляються.

Серединний перпендикуляр трикутника — це перпендикуляр, опущений на середину сторони трикутника. Три серединні перпендикуляри перетинаються в одній точці, яка є центром описаного кола. Діаметр описаного кола можна визначити з теореми синусів.
Виходячи з теореми Фалеса, можна стверджувати: якщо центр описаного кола розміщений на одній зі сторін трикутника, то протилежний кут — прямий. До того ж, якщо центр описаного кола розміщений всередині трикутника, то трикутник гострокутний, а якщо назовні, то трикутник тупокутний.

Висота трикутника — це пряма, проведена з вершини перпендикулярно до протилежної сторони або до продовження протилежної сторони. Ця сторона називається основою трикутника. Точка перетину сторони і перпендикуляра називається основою перпендикуляра. Довжина висоти — це відстань від вершини до основи трикутника. Три висоти перетинаються в одній точці, яка називається ортоцентром трикутника. Ортоцентр лежить всередині трикутника (і відповідно всі основи перпендикулярів лежать всередині трикутника) тоді і тільки тоді, якщо трикутник не тупокутний (у ньому жоден з внутрішніх кутів не більший від прямого кута). Див. також ортоцентрична система

Бісектриса трикутника — це пряма, проведена через вершину трикутника, яка ділить відповідний кут на дві рівні частини. Три бісектриси перетинаються в одній точці, інцентрі, центрі вписаного в трикутник кола. Вписане коло — це коло, яке лежить всередині трикутника і дотикається до трьох його сторін. Окрім того, є ще три важливі кола — зовнішні вписані; вони лежать за межами трикутника і дотикаються до одної його сторони, а також до продовження двох інших. Центри внутрішнього і зовнішніх вписаних кіл утворюють ортоцентричну систему.

Медіана трикутника — це пряма, проведена через вершину і середину протилежної сторони, вона ділить трикутник на два трикутники однакової площі. Три медіани перетинаються в одній точці, яка називається центроїдом трикутника. Ця точка є також центром мас трикутника: якби трикутник був зроблений з твердого матеріалу, то можна було б тримати рівновагу, тримаючи за центроїд. Центроїд ділить кожну медіану у співвідношенні , наприклад відстань між вершиною і центроїдом вдвічі більша ніж між центроїдом і протилежною стороною.

Середні точки трьох сторін і основи трьох висот лежать на одному колі, яке називається колом дев'яти точок трикутника. Решта три точки, через які коло отримало свою назву, — це середини тієї частини висоти, що лежить між ортоцентром і вершиною. Радіус кола дев'яти точок дорівнює половині описаного кола. Воно дотикається до вписаного кола (в точці Феєрбаха) та до трьох зовнішніх вписаних кіл.
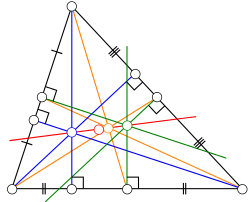
Центроїд (жовтий), ортоцентр (синій), центр описаного кола (зелений) і центр кола дев'яти точок (червона точка) — всі лежать на одній лінії, яка називається лінія Ейлера (червона лінія). Центр кола дев'яти точок лежить на середині між ортоцентром і центром описаного кола, а відстань між центроїдом і центром описаного кола дорівнює половині відстані між центроїдом та ортоцентром.
Основні факти

Вершини трикутника зазвичай позначають великими латинськими літерами , , , кути при відповідних вершинах грецькими літерами , , , а довжини протилежних сторін — маленькими латинськими літерами , , .
Сума внутрішніх кутів трикутника становить . Зовнішній кут трикутника (кут суміжний до внутрішнього кута) завжди дорівнює сумі двох інших внутрішніх кутів трикутника. Як і у всіх випуклих багатогранників, сума зовнішніх кутів трикутника .
Сума довжин двох будь-яких сторін трикутника завжди перевищує довжину третьої сторони. Це є нерівність трикутника, або аксіома трикутника (в окремому випадку нерівності два кути зменшуються до нуля і трикутник перетворюється у відрізок).
Два трикутники називають подібними тоді і тільки тоді, якщо кути одного рівні відповідним кутам іншого. В такому випадку довжини відповідних сторін пропорційні. Так може бути, наприклад, коли у двох трикутників є спільний кут, а сторони протилежні цьому куту — паралельні. Ось кілька постулатів і теорем про подібні трикутники:
- Два трикутники подібні, якщо в них хоча б два відповідні кути рівні.
- Якщо дві відповідні сторони в трикутниках пропорційні, а кут між ними однаковий, то трикутники подібні.
- Якщо всі сторони двох трикутників пропорційні, то трикутники подібні.
Два трикутники називають конгруентними, якщо всі їхні відповідні сторони і кути рівні (6 елементів). Кілька головних постулатів і теорем про конгруентні трикутники:
- Постулат SAS (side-angle-side): якщо дві сторони і кут між ними в трикутників відповідно рівні, то трикутники конгруентні.
- Постулат SSS: якщо всі відповідні сторони в трикутників рівні, то трикутники конгруентні.
- Постулат ASA: якщо сторона і прилеглі до неї кути в трикутників відповідно рівні, то трикутники конгруентні.
- Постулат AAS: якщо два кути і будь-яка сторона в трикутників відповідно рівні, то трикутники конгруентні.
- Теорема Гіпотенуза-катет: якщо гіпотенуза і один катет в прямокутних трикутників відповідно рівні, то трикутники конгруентні.
Обчислення площі трикутника

Обчислення площі трикутника є простою задачею, яку часто треба вирішити у багатьох галузях. Найвідоміша і найпростіша формула:
де — площа, — довжина основи трикутника, — висота трикутника, відносна до основи. Хоча ця формула й проста, вона може бути використана тільки у разі, якщо можна легко знайти висоту. Наприклад, землемір ділянки трикутної форми вимірює довжину кожної сторони і може знайти площу без визначення довжини висоти. На практиці можна використовувати різні методи визначення площі, залежно від того, що відомо про трикутник. Нижче наведено добірку найуживаніших формул.
З використанням векторів
Площу паралелограма можна обчислити за допомогою векторів. Нехай вектори і спрямовані відповідно від до і від до . Тоді площа паралелограма дорівнює , тобто числове значення векторного добутку і . дорівнює , де — висота паралелограма як вектор.
Площа трикутника дорівнює половині площі паралелограма .
Площу трикутника також можна обчислити як скалярний добуток векторів.
- .

Тригонометричний спосіб
Висоту трикутника можна визначити використовуючи тригонометричні формули. Згідно з позначенням, як на малюнку зліва, висота дорівнює . Підставивши висоту в формулу , яка наведена вище, отримаємо:
- .
Крім того, , що справедливо і для інших двох кутів:
- .
Знаючи сторону і два кути, один з яких прилеглий:
- ,
і аналогічно якщо відомі сторони a чи c.
Знаючи сторону і два прилеглі кути:[1]
- ,
і аналогічно якщо відомі сторони чи .
Використання координат
Якщо точка розташована в точці відліку Декартової координатної системи, а координати інших двох точок і , тоді площа може бути обчислена як абсолютного значення детермінанту:
- .
В загальнішому випадку:
- .
В тривимірному просторі площа трикутника {, і } дорівнює Піфагоровій сумі відповідних проєкцій на три головні площини (для яких або або ):
- .
Формула Герона
Форма трикутника однозначно визначається трьома сторонами. Відповідно для того, щоб порахувати площу, достатньо знати довжину сторін. За формулою Герона:
де — півпериметр
Інші способи запису формули Герона:
Формули, схожі на формулу Герона
Є три формули, що схожі на формулу Герона, але записані через інші величини. Позначивши медіани для сторін , , і відповідно як і , а їхню півсуму як , маємо[2]
Тоді, позначивши висоти на сторони , , і відповідно як , , і , і позначивши півсуму величин, обернених до висот, як , матимемо[3]
Позначивши півсуму синусів кутів як , матимемо[4]
де — діаметр описаного кола:
За допомогою теореми Піка
Див. теорему Піка для пояснень, як знайти площу довільного цілочислового многокутника.
Теорема стверджує, що
де — кількість цілочислових точок усередині многокутника, — кількість цілочислових точок на межі многокутника.
Інші формули обчислення площі
Існують також інші формули для обчислення площі, наприклад,
де — радіус вписаного кола, і - (півпериметр);
Для діаметра описаного кола ; і[5]
для кута .
В 1885 році, Бейкер[6] дав підбірку з більш ніж сотні різних формул для обчислення площі трикутника (хоча варто попередити читача, що деякі з них неправильні). Наводимо тут #9, #39a, #39b, #42, і #49:
- ,
- ,
- ,
Для радіуса описаного кола , і
- .
Обчислення площі прямокутного трикутника
У прямокутному трикутнику можна взяти один із катетів як основу, а інший — як його висоту. Звідси формула прямокутного трикутника
де — площа, а і — катети.
Обчислення сторін та кутів
Загалом, є різноманітні прийняті методи обчислення довжин сторін та кутів трикутника. Якщо певні методи можуть бути використані тільки в прямокутному трикутнику, то інші можуть виявитись потрібними для складніших випадків.
Тригонометричні відношення в прямокутних трикутниках

У прямокутних трикутниках тригонометричні співвідношення — синус, косинус і тангенс можуть використовуватись, щоб знайти невідомі кути чи невідомі довжини сторін. Сторони трикутника позначають так:
- Гіпотенуза — сторона протилежна до прямого кута, або найдовша сторона в прямокутному трикутнику, в даному випадку .
- Протилежний катет — сторона протилежна до кута, що розглядається.
- Прилеглий катет — та сторона, що прилягає до кута, що розглядається і до прямого. В даному випадку прилеглий катет .
Синус, косинус і тангенс
Синус кута — це відношення довжини протилежного катета до довжини гіпотенузи. В нашому випадку
- .
Зверніть увагу, що це співвідношення не залежить від конкретного вибраного прямокутного трикутника, якщо в ньому є кут , оскільки такі трикутники будуть подібні.
Косинус кута — це відношення довжини прилеглого катета до довжини гіпотенузи. В нашому випадку
Тангенс кута — це відношення довжини протилежного катета до довжини прилеглого. В нашому випадку
Обернені функції
Обернені тригонометричні функції використовують, щоб обчислити внутрішні кути прямокутного трикутника, якщо відомі довжини будь-яких двох сторін.
Arcsin використовують, щоб обчислити кут, якщо відомі довжина протилежної сторони і довжина гіпотенузи
Arccos використовують, щоб обчислити кут, якщо відомі довжина прилеглої сторони і довжина гіпотенузи
Arctan використовують, щоб обчислити кут, якщо відомі довжини протилежної та прилеглої сторони
На вступній геометрії та уроках тригонометрії, часто використовують позначення , , та ін. замість , тощо. Проте позначення , та інші є стандартними для вищої математики, де тригонометричні функції часто підносять до степеня, щоб не плутати обернений степінь з оберненою функцією.
Теореми синусів, косинусів та тангенсів

Теорема синусів, чи правило синусів,[7] стверджує що відношення довжин сторін до синусів відповідних протилежних кутів є величина стала, отже
- .
Це відношення дорівнює діаметру описаного кола даного трикутника. Інша інтерпретація теореми твердить, що кожен трикутник з кутами , і подібний до трикутника довжина сторін якого дорівнює , і . Цей трикутник може бути побудований, якщо накреслити коло діаметром і вписати в нього два кути вказаного трикутника. Довжина сторін трикутника буде , і . Сторона чия довжина протилежна до кута чия величина , і т. д.
Теорема косинусів, чи правило косинусів, поєднує довжину невідомої сторони трикутника з довжиною інших сторін і з кутом протилежним до невідомої сторони. Згідно з теоремою:
Для трикутника з довжинами сторін , , і кутами , , відповідно, для двох відомих довжин трикутника і , і кута між двома відомими сторонами (чи кута протилежного до невідомої сторони ), щоб розрахувати довжину третьої сторони можна використати наступну формулу:
Якщо довжина всіх трьох сторін трикутника відома, тоді кути можна розрахувати за формулами:
Теорема тангенсів, чи правило тангенсів, менш відома ніж два попередні. Вона стверджує:
Воно не дуже часто використовується, але може бути корисним коли потрібно знайти сторону чи кут, коли відомі дві сторони і кут чи два кути і сторона.
Ще формули для трикутників Евклідової геометрії
Для всіх трикутників Евклідової геометрії також справедливі такі формули:
і
- ,
і еквівалентно для і , з відповідними медіанами і сторонами;
для півпериметра , а довжина бісектриси вимірюється з вершини кута до точки перетину з протилежною стороною; в наступних формулах використовується радіус описаного кола та радіус вписаного кола :
якщо записати через висоти,
- ,
і
- .
Припустимо два суміжні трикутники, що не перетинаються, мають спільну сторону, довжина якої , і мають спільне описане коло таким чином, що сторона довжиною є хордою описаного кола; трикутники мають сторони з такими довжинами і , ці два трикутники разом утворюють вписаний чотирикутник, а його сторони відповідно . Тоді[8]
- .
Нехай — центроїд трикутника з вершинами , , і , і нехай — будь-яка внутрішня точка. Тоді відстані між цими точками пов'язані[8]
- .
Нехай , , і — відстані від центроїда до сторін , , і . Тоді[8]
і
- .
Неплощинні трикутники

Неплощинні трикутники — це трикутники, що розташовані не на (плоскій) площині. Прикладом такого трикутника в неевклідовій геометрії є сферичний трикутник, який вивчають у сферичній геометрії, та гіперболічний трикутник в гіперболічній геометрії.
Якщо сума внутрішніх кутів трикутника в площині завжди дорівнює , то для гіперболічного трикутника сума кутів буде меншою від , а для сферичного трикутника сума кутів буде більшою від . Гіперболічний трикутник можна отримати на негативно вигнутій поверхні, наприклад гіперболічний параболоїд, а сферичний трикутник можна отримати на позитивно вигнутій поверхні, наприклад сфера. Таким чином, якщо зобразити гігантський трикутник на поверхні Землі, то отримаємо суму кутів більшу ніж ; фактично сума буде лежати в проміжку і [9] Зокрема, можна зобразити трикутник на сфері таким чином, що кожен внутрішній кут буде дорівнювати , а сума всіх кутів .
Зокрема, на сфері сума кутів трикутника дорівнює
- ,
де — це відношення площі сфери до площі обмеженої трикутником. Наприклад, припустимо ми зобразимо трикутник на поверхні Землі (будемо вважати, що Земля це сфера, що насправді не зовсім так) з вершинами на Північному полюсі, на точці екватора з широтою , і точка на екваторі західної довготи. Лінія великого кола між згаданими двома точками буде екватор, а лінія великого кола між кожною з цих двох точок і Північним полюсом буде лінією меридіану; отже отримаємо прямі кути на екваторі. Більш того, кут на Північному полюсі також тому що попередні дві вершини різняться на за довготою. Сума кутів в цьому трикутнику — . Цей трикутник покриває північної півкулі ( якщо дивитись з Північного полюса) і відповідно земної поверхні, тоді підставляємо у формулу ; як бачимо, формула дає правильний результат .
З формули вище ми також бачимо, що в певному наближенні поверхню землі можна вважати плоскою: якщо зобразити довільний малий трикутник на поверхні Землі, тоді частка земної поверхні, яка обмежена даним трикутником буде близька до нуля. Наприклад, відомо що площа земної поверхні млн км², тоді для трикутника площею км², отримаємо суму кутів .
Див. також
- Гострий та тупий трикутники
- Тригонометричні функції
- Список тем про трикутник
- Одна сьома площі трикутника
- Теореми та твердження про трикутники
Примітки
- ↑ Weisstein, Eric W. Triangle(англ.) на сайті Wolfram MathWorld.
- ↑ Benyi, Arpad, "A Heron-type formula for the triangle, «Mathematical Gazette» 87, July 2003, 324—326.
- ↑ Mitchell, Douglas W., «A Heron-type formula for the reciprocal area of a triangle», Mathematical Gazette 89, November 2005, 494.
- ↑ Mitchell, Douglas W., «A Heron-type area formula in terms of sines», Mathematical Gazette 93, March 2009, 108—109.
- ↑ Mitchell, Douglas W., "The area of a quadrilateral", Mathematical Gazette 93, July 2009, 306—309.
- ↑ Baker, Marcus, "A collection of formulae for the area of a plane triangle, " Annals of Mathematics, part 1 in vol. 1(6), January 1885, 134—138; part 2 in vol. 2(1), September 1885, 11-18.
- ↑ Prof. David E. Joyce. The Laws of Cosines and Sines. Clark University. Архів оригіналу за 22 червня 2013. Процитовано 1 листопада 2008.
- ↑ а б в Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ. Co., 2007
- ↑ Watkins, Matthew, Useful Mathematical and Physical Formulae, Walker and Co., 2000.
Посилання
- Площа трикутника // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 82. — 594 с.
- Трикутник на сайті Formula.co.ua — математика для школи
- Геометрія, 7-9 класи. Трикутник на сайті «Острів знань».
- Формули для трикутника на сайті Geometry Atlas.(англ.)
- Кларк Кімберлінґ: Енциклопедія центрів трикутника. Список 3200 точок пов'язаних з трикутником.(англ.)
- Різні визначення для трикутника з інтерактивними додатками, які також можуть бути корисні для навчання в школі.(англ.)
- Інтерактивні демонстрації побудов трикутника з використанням циркуля та лінійки.(англ.)
- Трикутники: Теореми та проблеми. Інтерактивні ілюстрації на сайті Geometry from the Land of the Incas.(англ.)
- FIZMA.neT — Математика онлайн (Трикутник та його елементи)
- Трикут, трикутник // Українська мала енциклопедія : 16 кн. : у 8 т. / проф. Є. Онацький. — Накладом Адміністратури УАПЦ в Аргентині. — Буенос-Айрес, 1966. — Т. 8, кн. XV : Літери Ст — Уц. — С. 1931. — 1000 екз.
Література
- Г. П. Бевз. Геометрія трикутника. — Київ: Генеза, 2005, ISBN 966-504-431-1
- Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004, ISBN 966-7091-66-Х.
- І. А. Кушнір. Трикутник і тетраедр в задачах. — Київ: Радянська школа, 1991, ISBN 5-330-02081-6
- І. А. Кушнір. Повернення втраченої геометрії. — Київ: Факт, 2000 ISBN 966-7274-75-5
- Погорєлов О. В. Геометрія. Підручник. для 7 — 9 кл. — Київ: Школяр, 2004













































































![{\displaystyle P=[(\sin \ \ \alpha )+(\sin \ \ \beta )+(\sin \ \ \gamma )]/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12af5aa9e8ee2052542cc91e03eeabf1f0401c79)










![{\displaystyle S={\frac {1}{2}}[abch_{a}h_{b}h_{c}]^{1/3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9941182ec6acfa8d9ac06eeb392a6ae26a28ca1d)




























![{\displaystyle {\frac {a-b}{a+b}}={\frac {\tan[{\frac {1}{2}}(\alpha -\beta )]}{\tan[{\frac {1}{2}}(\alpha +\beta )]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b7a4a3592aa66976f1d34bbbb403daa392f9fdf)



![{\displaystyle {\text{Довжина внутрішньої бісектриси}}\ \ \alpha ={\frac {2{\sqrt {bcs(s-a)}}}{b+c}}={\sqrt {bc[1-{\frac {a^{2}}{(b+c)^{2}}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/468ef0355f7afac4c4c99854bb421a58f6ab89ab)




























