

Полікуб — об'емна фігура, утворена шляхом приєднання одного або більше однакових кубиків (сегментів) один до одного сторонами. Полікуби є тривимірним аналогом планарних полімін. Прикладами задач пакування-розміщення на основі полікубів є кубики сома, куб Бедлама, диявольський куб, головоломка Слотобера — Граатсми і головоломка Конвея.
Число полікубів
Як і у випадку з поліміно, кількість різноманітних варіантів залежить від умов достатньої різниці. Наприклад, чи вважати фігури утворені дзеркальними та поворотними перетвореннями тотожними початковим фігурам, чи ні. Наприклад, серед тетракубів існує 6 дзеркально-симетричних і один хіральний, які утворюють 7 вільних або 8 односторонніх. На відміну від поліміно, рахуючи полікуби, дзеркально перетворені фігури вважаються різними, оскеільки в просторі неможливо перетворити полікуб у його дзеркальне відображення.
| n | назва | число різноманітних полікубів | число вільних полікубів |
|---|---|---|---|
| 1 | монокуб | 1 | 1 |
| 2 | дікуб | 1 | 1 |
| 3 | трикуб | 2 | 2 |
| 4 | тетракуб | 8 | 7 |
| 5 | пентакуб | 29 | 23 |
| 6 | гексакуб | 166 | 112 |
| 7 | гептакуб | 1023 | 607 |
| 8 | октакуб | 6922 | 3811 |
Кевін Гонг знайшов кількість полікубів до 16 порядка.
Симетрії полікубів
Як і в разі поліміно, полікуби можуть бути класифіковані залежно від того, скільки у них є осей симетрії. Полікубічні симетрії (класи спряженості підгруп ахіраль восьмигранної групи) вперше були перераховані В. Ф. Лунноном у 1972. Більшість полікубів є асиметричними, але багато які з них мають більш складні групи симетрії, аж до повної групи симетрії куба з 48 елементами, також, наприклад, існує сім можливих форм 8-кратною симетрії.
Розгортки октокуба та гіперкуба
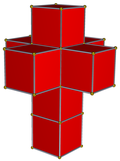
Тесеракт (чотиривимірний гіперкуб) складається з восьми кубів, що є його гранями, а тому, як куб може бути розгорнутим в гексамін, тесеракт може бути розгорнутим в октокуб. Тесеракт також може бути представлений у розгортці, що імітує відому розгортку куба в латинський хрест: він складається з чотирьох кубиків складених один поверх один одного та ще з чотирма кубиками, прикріплених до вільних квадратних граней другого зверху куба так, щоб сформувати тривимірний подвійний хрест. Сальвадор Далі використовував цю форму в його праці «Розп'яття» (1954), також вона описана в оповіданні Роберта А. Хайнлайна «І побудував він дім…» («Дім чотирьох вимірів»). На честь Далі, цей октокуб був названий хрест Далі.
Посилання
- Модель гексокуба зроблена Kadon [Архівовано 11 листопада 2016 у Wayback Machine.]
- симетрія полікубів[недоступне посилання з липня 2019]
- розв'язання полікубів[недоступне посилання з липня 2019]








