Сортування Шелла

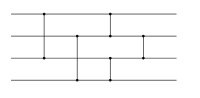
Демонстрація сортування Шелла з інтервалами 23, 10, 4, 1.
Клас	Алгоритм сортування
Структура даних	масив
Найгірша швидкодія	${\displaystyle \Omega (nlog^{2}n)}$
Оптимальний	Переважно ні

Сортува́ння Ше́лла — це алгоритм сортування, що є узагальненням сортування включенням.

Алгоритм базується на двох тезах:

• Сортування включенням ефективне для майже впорядкованих масивів.
• Сортування включенням неефективне, тому що переміщує елемент тільки на одну позицію за раз.

Тому сортування Шелла виконує декілька впорядкувань включенням, кожен раз порівнюючи і переставляючи елементи, що розташовані на різній відстані один від одного.

Сортування Шелла не є стабільним.

Сортування Шелла названо на честь автора — Дональда Шелла, який опублікував цей алгоритм у 1959^[1] році. В деяких пізніших друкованих виданнях алгоритм називають сортуванням Шелла-Мацнера, за ім'ям Нортона Мацнера. Але сам Мацнер стверджував: «Мені не довелось нічого робити з цим алгоритмом, і моє ім'я не має пов'язуватись з ним».^[2]

На початку обираються m-елементів: ${\displaystyle d_{1},d_{2},\dots ,d_{m}}$, причому, ${\displaystyle d_{1}>d_{2}>\dots >d_{m}=1}$.

Потім виконується m впорядкувань методом включення, спочатку для елементів, що стоять через ${\displaystyle \;d_{1}}$, потім для елементів через ${\displaystyle \;d_{2}}$ і т. д. до ${\displaystyle \;d_{m}=1}$.

Ефективність досягається тим, що кожне наступне впорядкування вимагає меншої кількості перестановок, оскільки деякі елементи вже стали на свої місця.

Сам алгоритм не залежить від вибору m і d, тому будемо вважати, що вони задані.

${\displaystyle Shell\_Sort(A,N)\;}$
1. for ${\displaystyle k\leftarrow 1}$ to ${\displaystyle \;m}$
2. do for ${\displaystyle i\leftarrow d[k]+1}$ to ${\displaystyle \;N}$
3.    do ${\displaystyle a\leftarrow A[i]}$
4.       ${\displaystyle j\leftarrow i}$
5.       while ${\displaystyle \;j-d[k]\geq 1}$ and ${\displaystyle \;A[j-d[k]]>a}$
6.       do ${\displaystyle A[j]\leftarrow A[j-d[k]]}$
7.          ${\displaystyle j\leftarrow j-d[k]}$
8.       ${\displaystyle A[j]\leftarrow a}$

Оскільки ${\displaystyle \;d_{m}=1}$ то на останньому кроці виконується звичайне впорядкування включенням всього масиву, а отже кінцевий масив буде впорядкованим.

Час роботи залежить від вибору значень елементів масиву d. Існує декілька підходів вибору цих значень:

• При виборі ${\displaystyle d_{1}=\left\lfloor {\frac {N}{2}}\right\rfloor ,d_{2}=\left\lfloor {\frac {d_{1}}{2}}\right\rfloor ,d_{3}=\left\lfloor {\frac {d_{2}}{2}}\right\rfloor ,\dots ,d_{m}=1}$ час роботи алгоритму, в найгіршому випадку, є ${\displaystyle \;O(N^{2})}$.
• Якщо d — впорядкований за спаданням набір чисел виду ${\displaystyle {\frac {3^{j}-1}{2}},j\in \mathbb {N} ,d_{i}<N}$, то час роботи є ${\displaystyle \;O\left(N^{\frac {3}{2}}\right)}$.
• Якщо d — впорядкований за спаданням набір чисел виду ${\displaystyle 2^{i}3^{j},i,j\in \mathbb {N} ,d_{k}<N}$, то час роботи є ${\displaystyle \;O(N\log ^{2}N)}$.
• Якщо d — впорядкований за спаданням набір чисел одного з видів:
  • ${\displaystyle 4^{k}+3\cdot 2^{k-1}+1,k\in \mathbb {N} }$ (з додатковим членом 1 на початку)
  • або ${\displaystyle {\begin{cases}9\left(2^{k}-2^{\frac {k}{2}}\right)+1&k{\text{ even}},\\8\cdot 2^{k}-6\cdot 2^{(k+1)/2}+1&k{\text{ odd}}\end{cases}}}$,

то час роботи алгоритму становить ${\displaystyle O\left(N^{\frac {4}{3}}\right)}$ (Sedgewick, 1986^[3]).

• Існують інші, оптимальніші послідовності, для яких не визначена верхня асимптотична оцінка, наприклад:
  • послідовність A102549 є найефективнішою з відомих, хоча формула для її визначення невідома (Ciura, 2001^[4]);
  • послідовність A108870 є найшвидшою з тих, що мають відому формулу: ${\displaystyle \left\lceil {\frac {1}{5}}\left(9\cdot \left({\frac {9}{4}}\right)^{k-1}-4\right)\right\rceil }$ (Tokuda, 1992^[5]).

Проілюструймо роботу алгоритму на вхідному масиві A = (5,16,1,32,44,3,16,7), d = (5,3,1).

1. Масив після впорядкування з кроком в 5: (3,16,1,32,44,5,16,7) — зроблено 1 обмін.
2. Масив після впорядкування з кроком 3: (3,7,1,16,16,5,32,44) — зроблено 3 обміни.
3. Масив після впорядкування з кроком 1: (1,3,5,7,16,16,32,44) — зроблено 5 обмінів.

Отже, весь масив впорядковано за 9 операцій обміну.

PROGRAM MyVerShellSort;
{$APPTYPE CONSOLE}
USES SysUtils;
TYPE massive=array[1..100] of integer;
VAR A:massive; n:integer;
procedure RndArrInput(var a1:massive; n1:integer);
  var i1:integer;
  begin
    randomize;
    for i1:=1 to n1 do
      a1[i1]:=10-random(20);
  end;
procedure Arroutput(a2:massive; n2:integer);
  var i2:integer;
  begin
    for i2:=1 to n2 do
      write(a2[i2],' ');
  end;
procedure change (var k,l:integer);
  var tmp:integer;
  begin
    tmp:=k; k:=l; l:=tmp;
  end;
procedure  ShellSort(var  A:massive;  N:integer);
  var  i,j,h:integer;
  begin
    h:=N  div  2;
    while  h>0  do
      begin
        for  i:=1  to  N-h  do
          begin
            j:=i;
            while  (j>=1)and(A[j]>A[j+h])  do
              begin
                change(a[j],a[j+h]);
                dec(j);
              end;
          end;
        h:=h  div  2;
      end;
  end;
BEGIN
writeln('enter data:');
readln(n);
RndArrInput(a,n);
ArrOutPut(a,n); readln;
ShellSort(a,n);
ArrOutPut(a,n);
readln;
END.

void sort_shell(int *a, int N)
{
    for (int d = N/2; d >= 1; d /= 2)
        for (int i = d; i < N; i++)
            for (int j = i; j >= d && a[j-d] > a[j]; j -= d)
                swap(a[j], a[j-d]);
}

• Наочна демонстрація сортування Шелла угорськими танцюристами.

Це незавершена стаття про алгоритми. Ви можете допомогти проєкту, виправивши або дописавши її.