Сере́днє сте́пеня p (середнє степеневе, узагальнене середнє) — узагальнення середнього арифметичного, середнього геометричного, середнього квадратичного, середнього гармонійного.
Якщо  — дійсне число не рівне нулю, можна визначити середнє степеня
— дійсне число не рівне нулю, можна визначити середнє степеня  для будь-яких додатних чисел
для будь-яких додатних чисел  як:
як:

Через граничний перехід довизначаються такі величини:
![{\displaystyle M_{0}(x_{1},\ldots ,x_{n})=\lim _{p\to 0}M_{p}(x_{1},\ldots ,x_{n})={\sqrt[{n}]{x_{1}\cdot \dots \cdot x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7f793292fa71c0e6b176f0bf55a8c038d8e8d90)


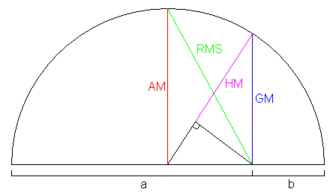 Геометричний зміст середніх значень для двох чисел.
Геометричний зміст середніх значень для двох чисел.
 — середнє гармонійне (HM),
— середнє гармонійне (HM),
![{\displaystyle M_{0}(x_{1},\dots ,x_{n})={\sqrt[{n}]{x_{1}\cdot \dots \cdot x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15811975b95408c4085cbc4a496cedc38f3767ba) — середнє геометричне (GM),
— середнє геометричне (GM),
 — середнє арифметичне (AM),
— середнє арифметичне (AM),
 — середнє квадратичне (RMS).
— середнє квадратичне (RMS).
- Якщо
 , тоді
, тоді  , і рівність наступає тільки при
, і рівність наступає тільки при  .
.
Це випливає з того, що  , що може бути доведено за допомогою нерівності Єнсена.
, що може бути доведено за допомогою нерівності Єнсена.
- Окремим випадком попередньої нерівності є:

|
|---|
| Середнє | |
|---|
| Геометрія | |
|---|
Теорія ймовірностей
та мат. статистика | |
|---|
| Теореми | |
|---|
| Нерівності | |
|---|













![{\displaystyle M_{0}(x_{1},\ldots ,x_{n})=\lim _{p\to 0}M_{p}(x_{1},\ldots ,x_{n})={\sqrt[{n}]{x_{1}\cdot \dots \cdot x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7f793292fa71c0e6b176f0bf55a8c038d8e8d90)



![{\displaystyle M_{0}(x_{1},\dots ,x_{n})={\sqrt[{n}]{x_{1}\cdot \dots \cdot x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15811975b95408c4085cbc4a496cedc38f3767ba)






