
Алгоритми створення лабіринту — це автоматичні методи для створення лабіринтів.
Методи теорії графів
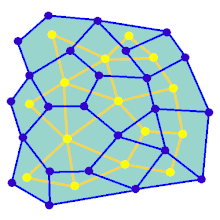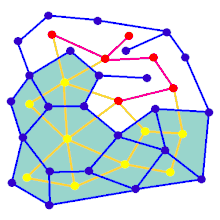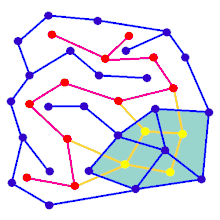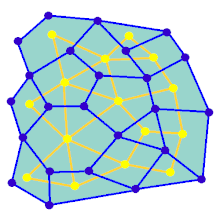
Лабіринт може бути створено, починаючи з заздалегідь визначеного розташування клітин (найчастіше прямокутної сітки, але можливі інші форми) зі стінками між ними. Ця наперед визначена домовленість може розглядатися як зв'язний граф з ребрами, що представляють можливі стінки, і вузлами, що представляють клітини. Призначенням алгоритму створення лабіринту можна вважати створення підграфу, в якому важко знайти шлях між двома окремими вузлами.
Якщо підграф не є зв'язним графом, то існують марні області графу, тому що вони не сприяють простору пошуку. Якщо граф містить петлі, то між вибраними вузлами може бути кілька шляхів. Через це, для створення лабіринтів часто звертаються до генерування випадкового кістякового дерева. Петлі, які можуть заплутати наївні алгоритми розв'язування лабіринтів, можуть бути введені шляхом додавання випадкових ребер до результату під час виконання алгоритму.
Анімація показує покрокове створення лабіринту по графу, який не розташований на прямокутній сітці. Спочатку комп'ютер створює випадковий планарний граф G, показаний синім кольором, а його двозв'язний граф F показано жовтим кольором. Потім комп'ютер проходить по F за допомогою обраного алгоритму, наприклад, такого як пошук у глибину, та зафарбовує шлях червоним. Під час обходу, коли червоне ребро перетинає синє ребро, синє ребро видаляється. Нарешті, коли всі вершини F будуть відвідані, видаляється F. Також, видаляються два ребра графу G, які використовуються для входу і для виходу.
Алгоритми на основі обходу графу
Пошук у глибину
Цей алгоритм є рандомізованою версією алгоритму пошуку у глибину. Часто реалізований з використанням стека, цей підхід є одним з найпростіших способів створення лабіринту за допомогою комп'ютера. Розглянемо простір для лабіринту, який є великою сіткою клітин (як велика шахова дошка), кожна комірка починається з чотирьох стін. Починаючи з випадкової клітинки, комп'ютер потім вибирає сусідню клітинку, яка ще не була відвідана. Комп'ютер видаляє стіну між двома клітинками і позначає нову клітинку як відвідану, і додає її до стека, щоб полегшити зворотне відтворення. Комп'ютер продовжує цей процес, і клітина, в якій немає невідвіданих сусідів, вважається тупиковим. Потрапивши у тупикову клітину, він відступає по шляху, поки не досягне клітини з невідвіданим сусідом, продовжуючи генерацію шляху, відвідавши цю нову, невідвідану клітинку (створюючи новий вузол). Цей процес триває до тих пір, поки не буде відвідано кожну клітину, що призведе до того, що комп'ютер повернеться назад до початкової клітини. Ми можемо бути впевнені, що кожна клітина відвідується.
Як зазначено вище, цей алгоритм передбачає глибоку рекурсію, яка може викликати проблеми з переповненням стека на деяких архітектурах комп'ютера. Цього можна уникнути, якщо використовувати явний стек. Нижче наведено два приклади на мові Java, які реалізують обидва варіанти. Алгоритм може бути представлений через цикл шляхом збереження інформації про зворотний порядок у самому лабіринті. Це також забезпечує швидкий спосіб зображення рішення, починаючи з будь-якої точки і повертаючи до початку.

Лабіринти, що генеруються завдяки пошуку у глибину, мають низький коефіцієнт розгалуження і містять багато довгих коридорів, тому що алгоритм досліджує, наскільки це можливо, по кожній гілці, перш ніж повернутись назад.
Алгоритм пошуку у глибину для створення лабіринтів часто реалізується за допомогою пошуку з вертанням:
- Зробіть початкову клітинку поточною клітиною та позначте її як відвідану
- У той час як є невідвідані клітини
- Якщо поточна клітина має сусідів, які не були відвідані
- Вибирайте випадково одного з невідвіданих сусідів
- Покладіть поточну клітину у стек
- Зніміть стінку між поточною клітиною і вибраною клітиною
- Зробіть вибрану клітину поточною клітиною та позначте її як відвідану
- Інакше, якщо стек не порожній
- Видаліть зі стека клітину
- Зробіть її поточною клітиною
- Якщо поточна клітина має сусідів, які не були відвідані
Рандомізований алгоритм Крускала
Цей алгоритм є рандомізованою версією алгоритму Крускала.
- Створіть список всіх стін і створіть набір для кожної клітини, кожна з яких містить тільки одну клітинку.
- Для кожної стіни, в якомусь випадковому порядку:
- Якщо клітини, розділені цією стіною, належать до різних наборів:
- Видаліть поточну стіну.
- Приєднуйтеся до наборів раніше розділених клітин.
- Якщо клітини, розділені цією стіною, належать до різних наборів:
Існує кілька структур даних, які можна використовувати для моделювання наборів клітин. Ефективна реалізація, що використовує структуру даних непересічної множини, може виконувати кожне об'єднання і знаходити операцію на двох наборах в майже сталий час (зокрема, складність часу ; для будь-якої правдоподібної величини ), тому час роботи цього алгоритму по суті пропорційний кількості стінок, доступних для лабіринту.
Незалежно від того, чи спочатку перелік стін рандомізований, або якщо стіна випадковим чином вибирається з невипадкового списку, так чи це інакше просто перекласти в формат коду.
Оскільки ефект цього алгоритму полягає у створенні мінімального кістякового дерева з графу з рівно зваженими ребрами, його метою є створення регулярних шаблонів, які достатньо легко вирішити.
Рандомізований алгоритм Прима
Цей алгоритм є рандомізованою версією алгоритму Прима.
- Почніть з сітки, повної стін.
- Виберіть клітинку, позначте її як частину лабіринту. Додайте стінки клітинки до списку стін.
- У той час як у списку є стіни:
- Виберіть випадкову стіну зі списку. Якщо відвідано лише одну з двох клітин, які розділяє стіна:
- Зробіть стіну проходом і позначте невідвідану клітинку як частину лабіринту.
- Додайте сусідні стіни клітинки до списку стін.
- Видаліть стіну зі списку.
- Виберіть випадкову стіну зі списку. Якщо відвідано лише одну з двох клітин, які розділяє стіна:
Як правило, відносно легко знайти шлях до стартової клітини, але важко знайти шлях де-небудь ще.
Зауважимо, що просто запуск класичного алгоритму Прима на графі з випадковими рельєфними вагами створить лабіринти, стилістично ідентичні алгоритму Крускала, тому що вони обидва є алгоритмами для побудування мінімального кістякового дерева. Замість цього, цей алгоритм вводить стилістичну варіацію, оскільки ребра, розташовані ближче до початкової точки, мають меншу ефективну вагу.
Модифікована версія
Хоча класичний алгоритм Прима зберігає список ребер, для генерації лабіринтів можна замість цього зберегти список сусідніх клітин. Якщо випадково обрана клітина має декілька ребер, які з'єднують її з лабіринтом, що існує, виберіть одне з цих ребер випадковим чином. Це, як правило, буде трохи більше, ніж вищезазначена версія на основі ребер.
Алгоритм Вільсона
Всі перераховані вище алгоритми мають різного роду зміщення: пошук у глибину зміщено у бік довгих коридорів, тоді як алгоритми Крускала/Прима зміщені до багатої кількості коротких тупиків. З іншого боку, алгоритм Вільсона[1] генерує незміщену вибірку з дискретним рівномірним розподілом над усіма лабіринтами, використовуючи випадковий пошук з виключенням циклічності.
Розпочнемо алгоритм, ініціалізуючи лабіринт однією довільно вибраною клітинкою. Потім ми починаємо з нової клітини, обраної довільно, і виконуємо випадковий пошук, поки не дістанемося до клітини, яка вже знаходиться в лабіринті — однак, якщо в будь-якій точці випадковий пошук досягне свого шляху, утворюючи петлю, ми виключаємо цикл з шляху перед тим, як продовжити. Коли шлях доходить до лабіринту, ми додаємо його до лабіринту. Потім ми виконуємо інший випадковий пошук з виключенням циклічності з іншої довільної початкової клітинки, повторюючи, поки всі клітини не будуть заповнені.
Ця процедура залишається неупередженою незалежно від того, який метод ми використовуємо для довільного вибору стартових клітинок. Отже, ми завжди можемо вибрати для простоти першу незаповнену клітинку (скажімо) зліва-направо, зверху вниз.
Метод рекурсивного поділу
| початкова камера | поділ двома стінками | отвори у стінках | продовження підподілу… | завершення |
|---|---|---|---|---|
 |
 |
 |
 |
 |
Лабіринти можуть бути створені за допомогою рекурсивного поділу, алгоритму, який працює наступним чином: Почніть з простору лабіринту без стін. Назвемо це камерою. Розділіть камеру випадково розташованою стінкою (або декількома стінами), де кожна стіна містить випадково розташований прохідний отвір. Потім рекурсивно повторіть процес на підкамерах, поки всі камери не будуть мінімальними. Цей метод призводить до того, що лабіринти з довгими прямими стінами перетинають їхній простір, що полегшує перегляд, які ділянки слід уникати.

Наприклад, у прямокутному лабіринті будують у випадкових точках дві стіни, перпендикулярні одна одній. Ці дві стіни ділять велику камеру на чотири менші камери, розділені чотирма стінами. Вибирають випадково три з чотирьох стін, і відкривають по одному отвору шириною з клітинку у випадковій точці в кожній з трьох. Продовжують таким чином рекурсивно, поки кожна камера не має ширину однієї клітини в одному з двох напрямків.
Прості алгоритми

Існують інші алгоритми, які вимагають достатньо пам'яті для зберігання однієї лінії 2D лабіринту або однієї площини 3D лабіринту.
Алгоритм Еллера запобігає петлям, зберігаючи які клітини в поточному рядку з'єднані через клітинки попередніх рядків, і ніколи не видаляє стінки між будь-якими двома вже з'єднаними клітинами.[2] Алгоритм бічного намотування починається з відкритого проходу по всьому верхньому рядку, а наступні рядки складаються з коротших горизонтальних проходів з одним включенням до проходу вище. Алгоритм бічного намотування тривіально вирішується знизу вгору, тому що він не має висхідних кінців.[3] Враховуючи початкову ширину, обидва алгоритми створюють ідеальні лабіринти необмеженої висоти.
Більшість алгоритмів генерації лабіринтів вимагають збереження зв'язків між клітинами всередині неї, щоб кінцевий результат був розв'язуваним. Проте можуть бути створені допустимі, просто пов'язані лабіринти, незалежно фокусуючись на кожній клітині. Бінарний деревуватий лабіринт — це стандартний ортогональний лабіринт, де кожна клітина завжди має прохід, що веде ліворуч або ліворуч, але ніколи не обидва. Щоб створити бінарний деревуватий лабіринт, для кожної клітинки киньте монетку, щоб вирішити, чи слід додати прохід, що веде вгору або вліво. Завжди вибирайте той самий напрямок для клітин на межі, а кінцевий результат буде валідний просто пов'язаним лабіринтом, який виглядає як бінарне дерево, при цьому верхній лівий кут буде його коренем. Як і в алгоритмі бічного намотування, бінарний лабіринт дерева не має мертвих кінців у напрямках зміщення.
Пов'язана форма перегортання монети для кожної клітинки полягає у створенні зображення за допомогою випадкового поєднання символів вперед, косих рис і зворотних рисок. Це не генерує валідний просто пов'язаний лабіринт, а скоріше вибір замкнутих петель і однокурсових уривків (посібник для Commodore 64 представляє програму мовою BASIC, яка використовує цей алгоритм, але використовує графічні символи PETSCII[en] діагональної лінії замість більш гладкого графічного вигляду).
Алгоритми клітинного автомата
Деякі типи клітинних автоматів можна використовувати для створення лабіринтів.[4] Два клітинних автомати відомих як, Maze і Mazectric, мають лінійки B3/S12345 і B3/S1234.[4] У першому це означає, що клітини виживають з однієї покоління до наступного, якщо у них є принаймні один і не більше п'яти сусідів Мура. В останньому це означає, що клітини виживають, якщо мають від одного до чотирьох сусідів. Якщо клітина має рівно трьох сусідів, вона народжується. Це схоже на автомат гра життя в тому, що структури, які не мають живої клітини, що прилягає до 1, 4 або 5 інших живих клітин у будь-якому поколінні, будуть поводитися ідентично до неї.[4] Однак для великих моделей він поводитися зовсім інакше, ніж в житті.[4], для великих моделей він поводитися зовсім інакше, ніж автомат гра життя.[4]
Для випадкового стартового шаблону ці клітинні автомати, що генерують лабіринт, перетворяться на складні лабіринти з чітко визначеними стінами, що викладають коридори. Mazecetric, що має правило B3/S1234, має тенденцію генерувати довші і прямі коридори у порівнянні з Maze, з правилом B3/S12345.[4] Оскільки ці правила клітинного автомата є детермінованими, кожен згенерований лабіринт однозначно визначається його випадковим початковим шаблоном. Це є суттєвим недоліком, оскільки лабіринти мають тенденцію бути відносно передбачуваними.
Як і деякі з описаних вище методів теорії графів, ці клітинні автомати зазвичай генерують лабіринти з одного початкового шаблону; отже, як правило, відносно легко знайти шлях до стартової клітини, але важче знайти шлях в іншому місці.
Приклад коду мовою Python
Приклад реалізації варіанту алгоритму Прима мовою Python. Вище зазначений алгоритм Прима починається з сітки, повної стін, і росте по одному компоненту прохідних плиток. У цьому прикладі ми починаємо з відкритої сітки і ростом кількох компонентів стін.
Цей алгоритм працює шляхом створення n (щільності) островів довжиною p (складність). Острів створюється вибором випадкової початкової точки з непарними координатами, потім вибирається випадковий напрямок. Якщо клітина на двох кроках вільна у напрямку, то в цьому напрямку додають стіну на одному кроці і на два кроки. Процес повторюється для n кроків для цього острова. Створюються острови. n і p виражаються як float для пристосування їх до розміру лабіринту. З низькою складністю острови дуже малі і лабіринт легко вирішити. З низькою щільністю лабіринт має більше «великих порожніх кімнат».
import numpy
from numpy.random import randint as rand
import matplotlib.pyplot as pyplot
def maze(width=81, height=51, complexity=.75, density=.75):
# Тільки непарні форми
shape = ((height // 2) * 2 + 1, (width // 2) * 2 + 1)
# Відрегулюємо складність і щільність щодо розміру лабіринту
complexity = int(complexity * (5 * (shape[0] + shape[1]))) # кількість компонентів
density = int(density * ((shape[0] // 2) * (shape[1] // 2))) # розмір компонентів
# Побудуємо справжній лабіринт
Z = numpy.zeros(shape, dtype=bool)
# Заповнюємо кордони
Z[0, :] = Z[-1, :] = 1
Z[:, 0] = Z[:, -1] = 1
# Зробимо проходи
for i in range(density):
x, y = rand(0, shape[1] // 2) * 2, rand(0, shape[0] // 2) * 2 # вибираємо випадкову позицію
Z[y, x] = 1
for j in range(complexity):
neighbours = []
if x > 1: neighbours.append((y, x - 2))
if x < shape[1] - 2: neighbours.append((y, x + 2))
if y > 1: neighbours.append((y - 2, x))
if y < shape[0] - 2: neighbours.append((y + 2, x))
if len(neighbours):
y_,x_ = neighbours[rand(0, len(neighbours) - 1)]
if Z[y_, x_] == 0:
Z[y_, x_] = 1
Z[y_ + (y - y_) // 2, x_ + (x - x_) // 2] = 1
x, y = x_, y_
return Z
pyplot.figure(figsize=(10, 5))
pyplot.imshow(maze(80, 40), cmap=pyplot.cm.binary, interpolation='nearest')
pyplot.xticks([]), pyplot.yticks([])
pyplot.show()
Приклад коду мовою Java
Приклад реалізації алгоритму рандомізованого пошуку у глибину.
RandomizedDFS.java:
package de.amr.maze.simple;
import java.util.ArrayDeque;
import java.util.BitSet;
import java.util.Deque;
import java.util.Random;
/**
* Створює лабіринт з графу сітки, використовуючи рандомізований пошук у глибину.
*
* @author Armin Reichert
*/
public class RandomizedDFS{
public static void main(String[] args) {
// Використання рекурсивної процедури:
System.out.println(maze(10, 10, 0, 0, true));
// Використання нерекурсивної процедури:
System.out.println(maze(10, 10, 0, 0, false));
}
/** Повертає лабіринт заданого розміру початкової генерації в даній позиції сітки. */
public static Grid maze(int numCols, int numRows, int startCol, int startRow, boolean recursive) {
Grid grid = new Grid(numCols, numRows);
BitSet visited = new BitSet(numCols * numRows);
if (recursive) {
traverseRecursive(grid, grid.vertex(startCol, startRow), visited);
}
else {
traverseUsingStack(grid, grid.vertex(startCol, startRow), visited);
}
return grid;
}
/** Рекурсивна процедура, що проходить через сітку і створює лабіринт (кістякове дерево). */
private static void traverseRecursive(Grid grid, int v, BitSet visited) {
visited.set(v);
for (int dir = unvisitedDir(grid, v, visited); dir != -1; dir = unvisitedDir(grid, v, visited)) {
grid.addEdge(v, dir);
traverseRecursive(grid, grid.neighbor(v, dir), visited);
}
}
/** Нерекурсивна процедура, що проходить через сітку і створює лабіринт (кістякове дерево). */
private static void traverseUsingStack(Grid grid, int v, BitSet visited) {
Deque<Integer> stack = new ArrayDeque<>();
visited.set(v);
stack.push(v);
while (!stack.isEmpty()) {
int dir = unvisitedDir(grid, v, visited);
if (dir != -1) {
int neighbor = grid.neighbor(v, dir);
grid.addEdge(v, dir);
visited.set(neighbor);
stack.push(neighbor);
v = neighbor;
}
else {
v = stack.pop();
}
}
}
/** Повертає випадковий напрямок невідомому сусіду або -1. */
private static int unvisitedDir(Grid grid, int v, BitSet visited) {
int[] candidates = new int[4];
int numCandidates = 0;
for (int dir : new int[] { Grid.NORTH, Grid.EAST, Grid.SOUTH, Grid.WEST }) {
int neighbor = grid.neighbor(v, dir);
if (neighbor != Grid.NO_VERTEX && !visited.get(neighbor)) {
candidates[numCandidates++] = dir;
}
}
return numCandidates == 0 ? -1 : candidates[new Random().nextInt(numCandidates)];
}
}
Grid.java:
package de.amr.maze.simple;
import java.util.BitSet;
/**
* Реалізація сітки графу. Набір ребер представлений одним набором бітів.
*/
public class Grid {
/** Напрямки. */
public static final int NORTH = 0, EAST = 1, SOUTH = 2, WEST = 3;
/** Протилежні напрямки. */
public static final int[] OPPOSITE = { SOUTH, WEST, NORTH, EAST };
/* Напрямні вектори. */
public static final int[] X = { 0, 1, 0, -1 };
public static final int[] Y = { -1, 0, 1, 0 };
/** Індекс не представляє вершини. */
public static final int NO_VERTEX = -1;
/** Кількість стовпців сітки. */
public final int numCols;
/** Кількість рядків сітки. */
public final int numRows;
private BitSet edges;
/** Індекс бітового набору ребра, що залишає вершину v до напрямку dir. */
private int bit(int v, int dir) {
return 4 * v + dir;
}
/** Створює порожню сітку заданого розміру. */
public Grid(int numCols, int numRows) {
this.numCols = numCols;
this.numRows = numRows;
edges = new BitSet(numCols * numRows * 4);
}
/** Вершина в колонці col і в рядку row. */
public int vertex(int col, int row) {
return numCols * row + col;
}
/** Стовпчик вершини v. */
public int col(int v) {
return v % numCols;
}
/** Рядок вершини v. */
public int row(int v) {
return v / numCols;
}
/** Повертає кількість (неорієнтованих) ребер. */
public int numEdges() {
return edges.cardinality() / 2;
}
/** Додає ребро з вершини v до напрямку dir. */
public void addEdge(int v, int dir) {
edges.set(bit(v, dir));
edges.set(bit(neighbor(v, dir), OPPOSITE[dir]));
}
/** Вказує, чи ребро від вершини v до напрямку dir існує. */
public boolean hasEdge(int v, int dir) {
return edges.get(bit(v, dir));
}
/**
* Повертає сусіда вершини v до напрямку dir або #NO_VERTEX.
*/
public int neighbor(int v, int dir) {
int col = col(v) + X[dir], row = row(v) + Y[dir];
return col >= 0 && col < numCols && row >= 0 && row < numRows ? vertex(col, row) : NO_VERTEX;
}
/** Повертає текстове представлення цієї сітки. */
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
for (int row = 0; row < numRows; ++row) {
for (int col = 0; col < numCols; ++col) {
sb.append(String.format("[%2d,%2d]", row, col));
sb.append(col < numCols - 1 && hasEdge(vertex(col, row), EAST) ? "--" : " ");
}
if (row < numRows - 1) {
sb.append("\n");
for (int col = 0; col < numCols; ++col) {
sb.append(hasEdge(vertex(col, row), SOUTH) ? " {{!}} ": " ");
}
sb.append(«\n»);
}
}
sb.append(String.format(«\n\n[%d cols, %d rows, %d edges]\n», numCols, numRows, numEdges()));
return sb.toString();
}
}
Приклад коду мовою С
Нижче наведено приклад алгоритму пошуку в глибину для створення лабіринту мовою С.
//Код написано Яцеком Вічореком
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
typedef struct
{
int x, y; //Позиція вузла - мала витрата пам'яті, але сприяє швидшому генеруванню
void *parent; //Покажчик на батьківський вузол
char c; //Символ для відображення
char dirs; //Напрямки, які ще не визначені
} Node;
Node *nodes; //Масив вузлів
int width, height; //Розміри лабіринту
int init( )
{
int i, j;
Node *n;
//Виділення пам'яті для лабіринту
nodes = calloc( width * height, sizeof( Node ) );
if ( nodes == NULL ) return 1;
//Встановлення важливих вузлів
for ( i = 0; i < width; i++ )
{
for ( j = 0; j < height; j++ )
{
n = nodes + i + j * width;
if ( i * j % 2 )
{
n->x = i;
n->y = j;
n->dirs = 15; //Припустимо, що всі напрямки можна дослідити
//(встановлено 4 наймолодших біти)
n->c = ' ';
}
else n->c = '#'; //Додаємо стінки між вузлами
}
}
return 0;
}
Node *link( Node *n )
{
//Підключаємо вузол до випадкового сусіда (якщо можливо) і повертаємо
//адресу наступного вузла, який слід відвідати
int x, y;
char dir;
Node *dest;
//Нічого не можна зробити, якщо задано нульовий покажчик - вихід
if ( n == NULL ) return NULL;
//Поки є напрямки досі невизначені
while ( n->dirs )
{
//Довільно вибирається один напрямок
dir = ( 1 << ( rand( ) % 4 ) );
//Якщо його вже було досліджено - спробуйте ще раз
if ( ~n->dirs & dir ) continue;
//Позначимо напрямок як досліджений
n->dirs &= ~dir;
//Залежно від обраного напрямку
switch ( dir )
{
//Перевіряємо, чи можна йти праворуч
case 1:
if ( n->x + 2 < width )
{
x = n->x + 2;
y = n->y;
}
else continue;
break;
//Перевіряємо, чи можна спуститися
case 2:
if ( n->y + 2 < height )
{
x = n->x;
y = n->y + 2;
}
else continue;
break;
//Перевіряємо, чи можна йти ліворуч
case 4:
if ( n->x - 2 >= 0 )
{
x = n->x - 2;
y = n->y;
}
else continue;
break;
//Перевіряємо, чи можна піднятися
case 8:
if ( n->y - 2 >= 0 )
{
x = n->x;
y = n->y - 2;
}
else continue;
break;
}
//Отримаємо вузол призначення через покажчик (що робить речі трохи швидшими)
dest = nodes + x + y * width;
//Переконаємося, що вузол призначення не є стіною
if ( dest->c == ' ' )
{
//Якщо призначення вже є зв'язаним вузлом - перервати
if ( dest->parent != NULL ) continue;
//В іншому випадку прийняти вузол
dest->parent = n;
//Видалення стінки між вузлами
nodes[n->x + ( x - n->x ) / 2 + ( n->y + ( y - n->y ) / 2 ) * width].c = ' ';
//Повернення адреси дочірнього вузла
return dest;
}
}
//Якщо нічого більше тут не можна зробити - повернемо батьківську адресу
return n->parent;
}
void draw( )
{
int i, j;
//Вихідні дані лабіринту до терміналу - нічого особливого
for ( i = 0; i < height; i++ )
{
for ( j = 0; j < width; j++ )
{
printf( "%c", nodes[j + i * width].c );
}
printf( "\n" );
}
}
int main( int argc, char **argv )
{
Node *start, *last;
//Перевірка кількості аргументів
if ( argc < 3 )
{
fprintf( stderr, "%s: please specify maze dimensions!\n", argv[0] );
exit( 1 );
}
//Читання розмірів лабіринту з аргументів командного рядка
if ( sscanf( argv[1], "%d", &width ) + sscanf( argv[2], "%d", &height ) < 2 )
{
fprintf( stderr, "%s: invalid maze size value!\n", argv[0] );
exit( 1 );
}
//Дозволяємо лише непарні розміри
if ( !( width % 2 ) {{!}}{{!}} !(height % 2) )
{
fprintf( stderr, «%s: dimensions must be odd!\n», argv[0] );
exit( 1 );
}
//Не допускаємо від'ємних розмірів
if ( width <= 0 {{!}}{{!}} height <= 0 )
{
fprintf( stderr, «%s: dimensions must be greater than 0!\n», argv[0] );
exit( 1 );
}
//Насінний випадковий генератор
srand(time(NULL));
//Ініціалізація лабіринту
if ( init() )
{
fprintf( stderr, «%s: out of memory!\n», argv[0] );
exit( 1 );
}
//Встановлення початкового вузла
start = nodes + 1 + width;
start->parent = start;
last = start;
//Підключаємо вузли до тих пір, поки не буде досягнутий початковий вузол і
//не буде покинутим
while ((last = link(last)) != start);
draw();
}
Див. також
Примітки
- ↑ Вільсон, Девід Брюс (22–24 Травня 1996). Створення охоплюючих випадкових дерев швидше, ніж за час покриття. Симпозіум з теорії обчислень. Філадельфія: ACM. с. 296—303. doi:10.1145/237814.237880. ISBN 0-89791-785-5. Архів оригіналу (PDF) за 14 травня 2013. Процитовано 30 квітня 2019.
- ↑ Джеміс Бак (29 Грудня 2010). Створення лабіринту: алгоритм Ейлера. Архів оригіналу за 28 квітня 2019. Процитовано 30 квітня 2019.
- ↑ Джеміс Бак (3 Лютого 2011). Створення лабіринту: Алгоритм бічного намотування. Архів оригіналу за 3 травня 2019. Процитовано 30 квітня 2019.
- ↑ а б в г д е Nathaniel Johnston та ін. (21 Серпня 2010). Maze - LifeWiki. LifeWiki. Архів оригіналу за 14 грудня 2013. Процитовано 1 Березня 2011.
Посилання
- Думайте про лабіринт: алгоритми лабіринту [Архівовано 6 квітня 2019 у Wayback Machine.] (подробиці щодо цих та інших алгоритмів генерації лабіринту)
- Джеміс Бак: HTML 5 Презентація з demo версіями алгоритмів створення лабіринтів [Архівовано 28 квітня 2019 у Wayback Machine.]
- Візуалізація генерування лабіринтів [Архівовано 13 лютого 2020 у Wayback Machine.]
- Реалізація мовою Java алгоритму Прима [Архівовано 24 квітня 2019 у Wayback Machine.]
- Реалізація алгоритму пошуку в глибину для створення лабіринту [Архівовано 26 квітня 2019 у Wayback Machine.] декількома мовами в Rosetta Code
- Армін Рейхерт: 34 алгоритми створення лабіринту мовою Java 8, з демо-додатками [Архівовано 12 червня 2018 у Wayback Machine.]
- CADforum: алгоритм створення лабіринту в VisualLISP [Архівовано 14 вересня 2018 у Wayback Machine.]
- Кодовий виклик #10.1: Генератор лабіринтів з p5.js — Частина 1: Алгоритм створення лабіринту в JavaScript з p5 [Архівовано 25 червня 2020 у Wayback Machine.]
- Генератор лабіринтів Чарльза Бонда, COMPUTE! Журнал, Грудень 1981











